Do pai dos ignorantes desesperados por uma resposta rápida, Wikipedia...
Nem dá para imaginar a sequencia de fórmulas e letras esquisitas no meio das palavras… Junto com a citação de um cara chamado Poincaré. Eu já meio que entendi que qdo este nome está no meio de um monte de teorias.. a coisa é punk. Bem punk. Como disse uma amiga matemática, Rock'n Roll!!!!!
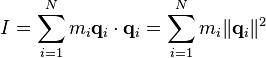- nem consigo imaginar o que seja…Enfim…
Isto, ao meu ver, caracteriza a dificuldade teórica que temos ao tentar prever a harmonia entre seres diferentes. Ou, a chegada de um "corpo estranho" numa dinâmica social familiar pré-estabelecida.
Por vezes batemos tanto, mas tanto nesta tecla que empacamos.
Desconsideramos a força da Natureza que consegue sim estabelecer uma harmonia entre os corpos celestes.
Entre os seres humanos… cada um com suas convicções, desejos, aspirações, características tão, mas tão diversas… Acho que algo sempre pode nos pegar de surpresa:
Vai chegando devagarinho ao som da melodia,
emitindo pseudópodes que encontram as pequenas frestas
naquela esfera antes hermética
pseudohermética!!!
De repente percebemos o rearranjo,
a harmonia entre os corpos celestes
Como pode ser tão natural?!?!?!
Nenhum comentário:
Postar um comentário